前缀和+差分

前缀和对我来说已经不算陌生了，前缀和的方便之处在于可以 快速求解任意子数组之和。但是，前缀和在区间频繁修改时就显得较为羸弱了，因为它只适合求和，不擅长修改。

那么，如果某些区间频繁修改（仅限于都增加或者都减少某个值），但是求和只有一次，这种时候首先会想到的就是线段树了，不过线段树的代码量太多，使用差分则更简单，也更快。

什么是差分？

差分的意思主要是这个 差，指的其实就是 元素差。

前缀和的思想是动态规划，可以将前 n 个元素的和预先存储起来，这样计算区间和的时候就不需要再按需进行累加了。

而差分的思想就是 先求出相邻元素之间的差，当需要某个区间[a,b]增加或者减少某个值的，只需要修改 arr[a] 和 arr[b+1]，然后重新计算一次前缀和就可以了。

一维数组差分

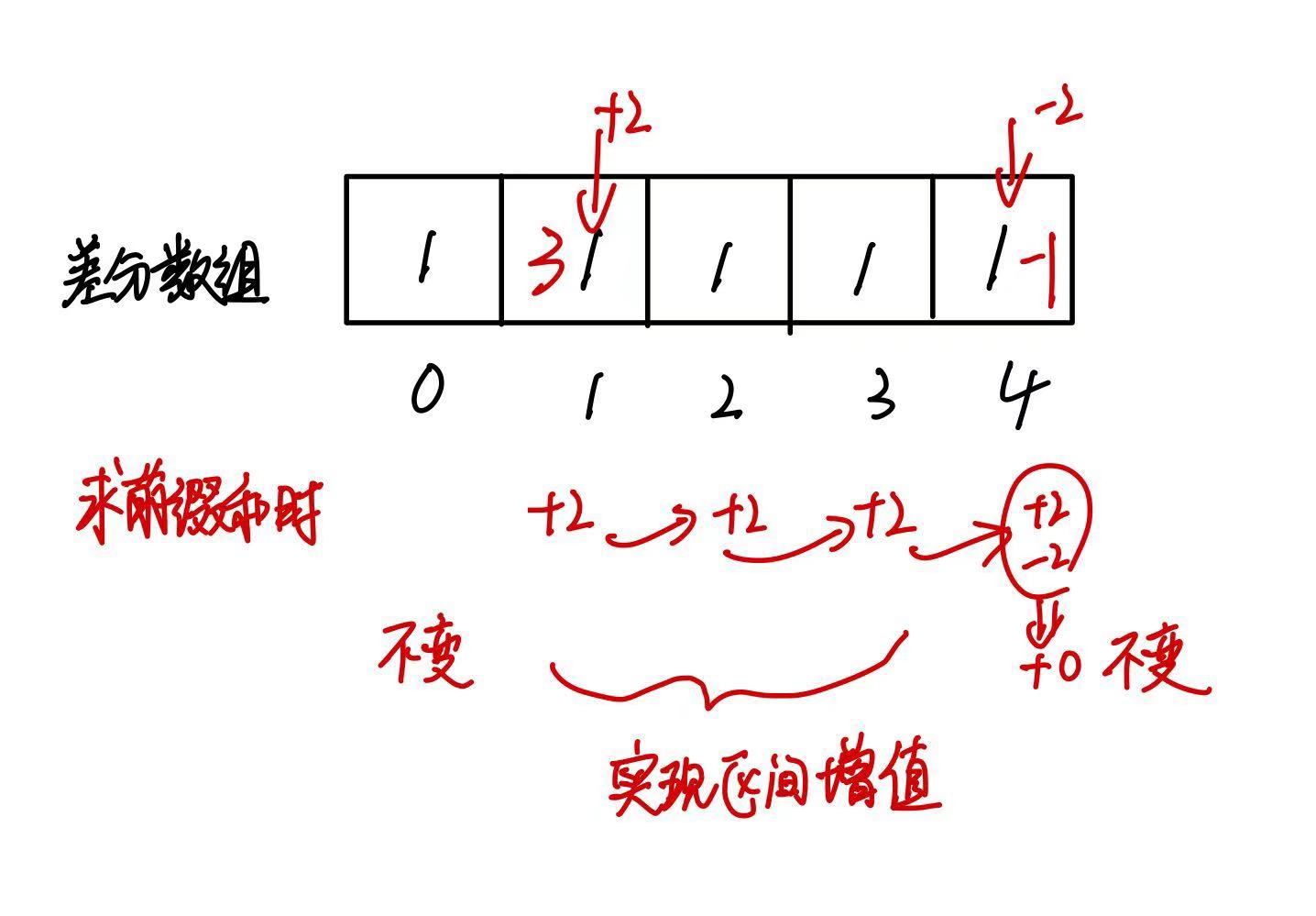
如果有一个数组 [1, 2, 3, 4, 5]，其差分数组为 [1, 1, 1, 1, 1]。如果要将区间 [1, 3] 中的每个元素增加 2，可以通过修改差分数组 diff[1] += 2 和diff[4] -= 2来实现，得到新的差分数组[1, 3, 1, 1, -1]。通过重建数组可以得到[1, 4, 5, 6, 5]。

树上差分

刚才只是在一维数组上差分，实现起来还是比较简单的，如果我们是在树上进行差分呢？
树上差分刚才只是在一维数组上差分，实现起来还是比较简单的，如果我们是在树上进行差分呢？

场景：现在给你一颗树，并且告诉你起始节点和结束节点，对起始节点和结束节点路径中的所有节点的值都加上value。需要注意的是，这里的树指的是一颗无向树，也就是说并不是像只能从父节点向子节点的那种遍历，只要是这个节点连接到的结点，都是可以遍历到的。

如果要使用树上差分，就必不可免要使用到树中节点的 最近公共祖先 求解算法。[[最近公共祖先（LCA)]] 。关于LCA的求解推荐使用倍增法，可以详细看看。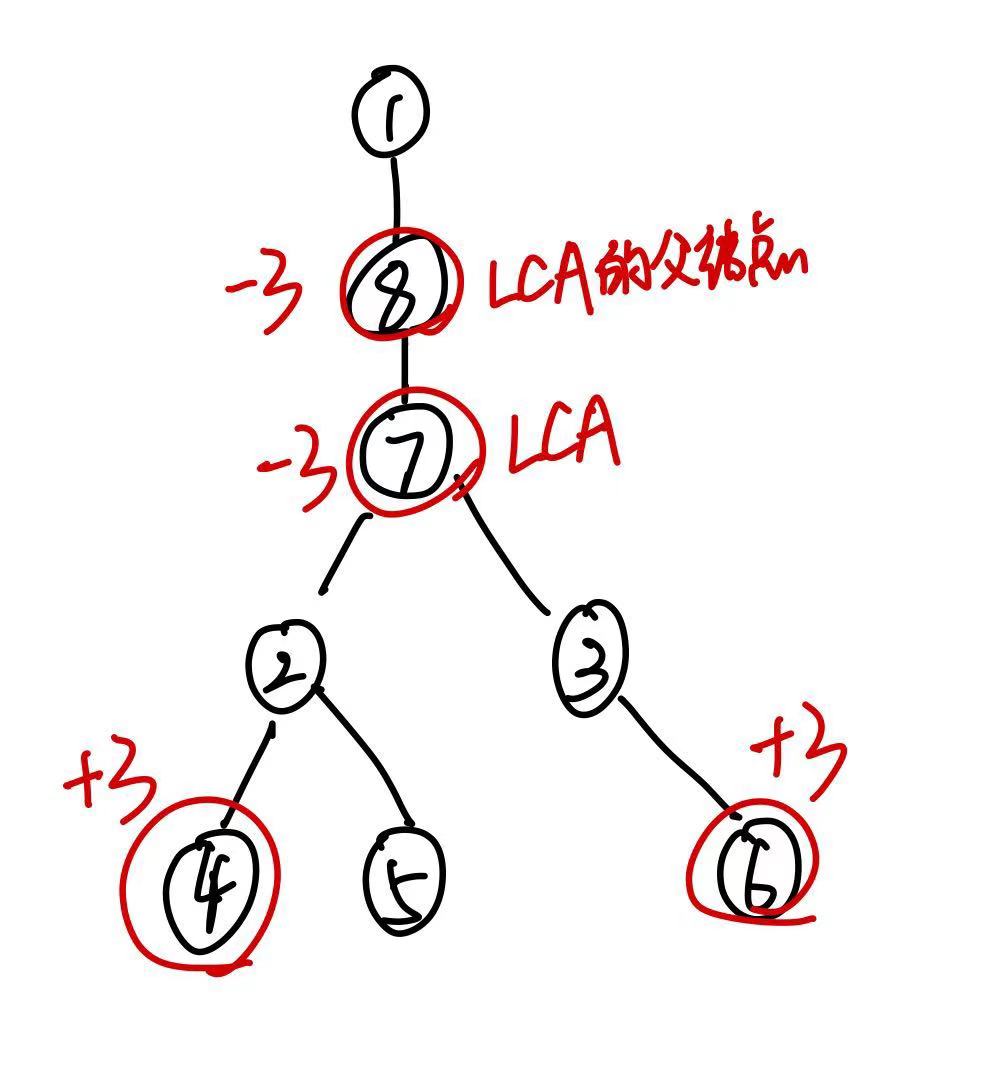

如图所示，实现差分我们只需要修改四个点的权值，起始点和终结点就不用说了，关键是这个 LCA还有LCA的父节点。这里你可能会有如下问题：

Note

为什么这里还要将LCA的父节点权值也下降？

原因是我们从根节点1开始进行DFS，原本的前缀和在这里更像“后缀和”。
DFS的过程中，每个节点的权值更新为其所有子孙的权值总和，weight[i]=

对于LCA本身，其本身只需要+3，不过a和b都是他的子孙，所以其本身-3。对于LCA的父节点，他的权值应该是不变的，刚才LCA减去3是因为LCA要+3，但是LCA的父节点应该是不变的，因此LCA的父节点权值也需要下降。

using LL = long long;
class Solution {
    public: int maxRemoval(vector < int > & nums, vector < vector < int >> & queries) {
        // sort(queries.begin(), queries.end(), [](vector<int>&a, vector<int>&b){
        //     if (a[0]!=b[0])
        //         return a[0]<b[0];
        //     else
        //         return a[1]>b[1];
        // });
        sort(queries.begin(), queries.end());

        int n = nums.size();
        int j = 0;
        vector < int > diff(n + 1);
        LL sum = 0;
        int ret = 0;
        priority_queue < int > pq;
        for (int i = 0; i < n; i++) {
            while (j < queries.size() && queries[j][0] <= i) {
                pq.push(queries[j][1]);
                j++;
            }
            while (sum + diff[i] < nums[i]) {
                if (pq.empty()) return -1;
                if (pq.top() < i) return -1;
                int t = pq.top();
                pq.pop();
                sum += 1;
                diff[t + 1] -= 1;
                ret++;
            }
            sum += diff[i];
        }
        return queries.size() - ret;
    }

};